Recent posts
Neural Ordinary Differential Equations
A significant portion of processes can be described by differential equations: let it be evolution of physical systems, medical conditions of a patient, fundamental properties of markets, etc. Such data is sequential and continuous in its nature, meaning that observations are merely realizations of some continuously changing state.
There is also another type of sequential data that is discrete – NLP data, for example: its state changes discretely, from one symbol to another, from one word to another.
Today both these types are normally processed using recurrent neural networks. They are, however, essentially different in their nature, and it seems that they should be treated differently.
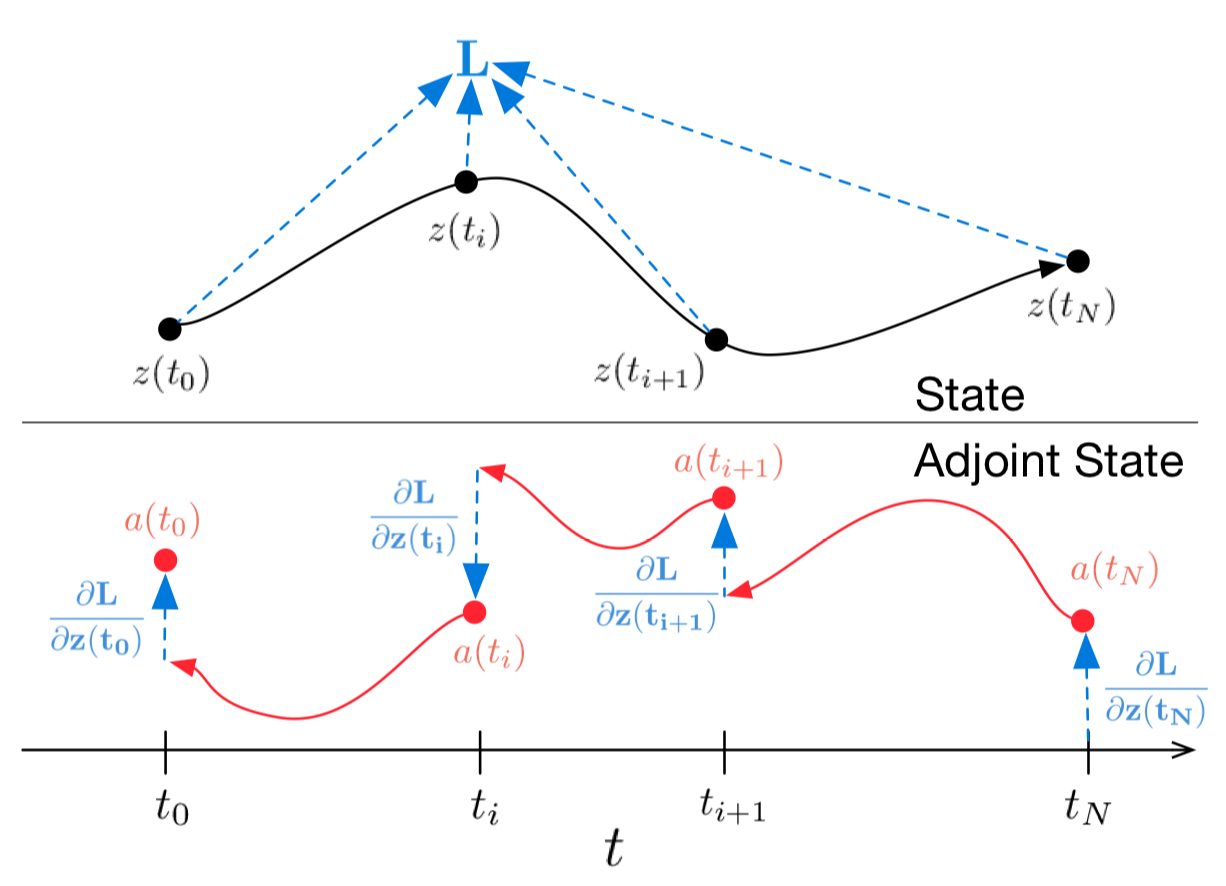
At the last NIPS conference a very interesting paper was presented that attempts to tackle this problem. Authors propose a very promising approach, which they call Neural Ordinary Differential Equations.
Here I tried to reproduce and summarize the results of original paper, making it a little easier to familiarize yourself with the idea. As I believe, this new architecture may soon be, among convolutional and recurrent networks, in a toolbox of any data scientist.
Generative models collection
PyTorch implementations of various generative models to be trained and evaluated on CelebA dataset. The models are: Deep Convolutional GAN, Least Squares GAN, Wasserstein GAN, Wasserstein GAN Gradient Penalty, Information Maximizing GAN, Boundary Equilibrium GAN, Variational AutoEncoder and Variational AutoEncoder GAN. All models have as close as possible nets architectures and implementations with necessary deviations required by their articles.
ContinueAutoEncoders in Keras: VAE-GAN
In the previous part, we created a CVAE autoencoder, whose decoder is able to generate a digit of a given label, we also tried to create pictures of numbers of other labels in the style of a given picture. It turned out pretty good, but the numbers were generated blurry.
In the last part, we studied how the GANs work, getting quite clear images of numbers, but the possibility of coding and transferring the style was lost.
In this part we will try to take the best from both approaches by combining variational autoencoders (VAE) and generative competing networks (GAN).
The approach, which will be described later, is based on the article [Autoencoding beyond pixels using a learned similarity metric, Larsen et al, 2016].
AutoEncoders in Keras: VAE
In the last part, we have already discussed what hidden variables are, looked at their distribution, and also understood that it is difficult to generate new objects from the distribution of latent variables in ordinary autoencoders. In order to be able to generate new objects, the space of latent variables must be predictable.
Variational Autoencoders are autoencoders that learn to map objects into a given hidden space and sample from it. Therefore, variational autoencoders are also referred to the family of generative models.
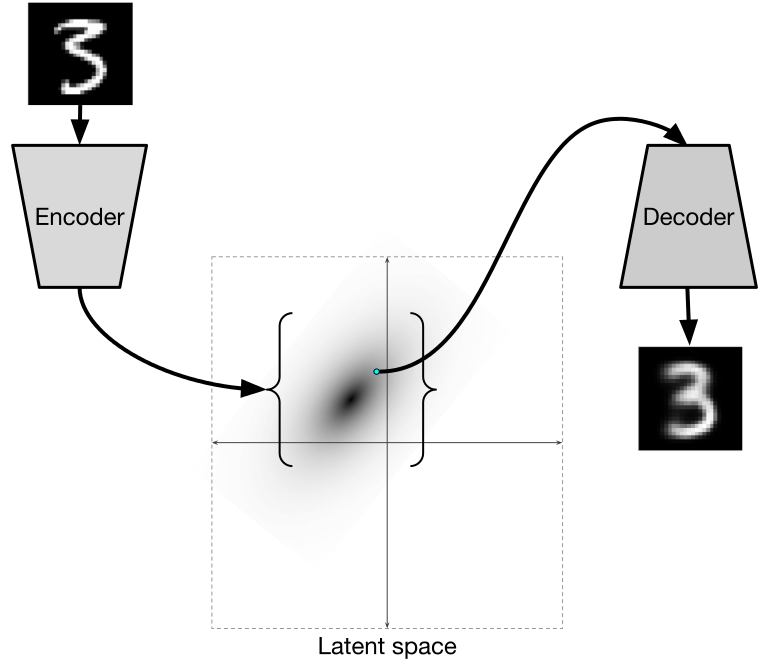Illustration from here
AutoEncoders in Keras: Manifold learning and latent variables
In order to better understand how autoencoders work, and also to subsequently generate something new from codes, it is worth understanding what codes are and how they can be interpreted.
AutoEncoders in Keras: Introduction
While diving into Deep Learning, the topic of auto-encoders caught me, especially in terms of generating new objects. In an effort to improve the quality of generation, I read various blogs and literature on the topic of generative approaches. As a result, I decided to reflect the gained experience in a small series of articles, in which I tried briefly and with examples to describe all those problem areas I had encountered myself, while at the same time introducing to Keras.
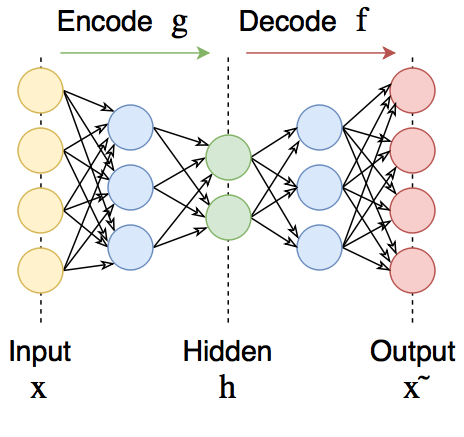
AutoEncoders in Keras: GAN
With all the advantages of VAE variational autoencoders, which we dealt with in previous posts, they have one major drawback: due to the poor way of comparing original and restored objects, the objects they generated are similar to the objects from the training set, but they are easily distinguishable from them (for example blurred).
This disadvantage is much less pronounced in another approach, namely, generative competing networks - GANs.
(The real reason why VAEs produce blurred images is because of the way we define likelihood when comparing original and restored object. Namely, we suppose that pixel values are independent from each other (likelihood factorizes into product of likelihoods for each pixel). GANs don’t make this assumption (because we don’t define the likelihood at all), and thus are not restricted by it.)
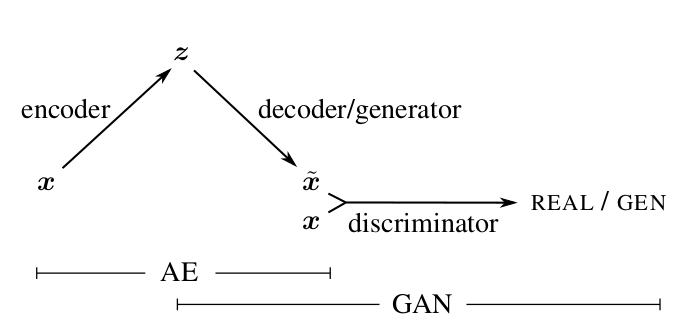
Formally, GANs, of course, do not belong to autoencoders, however there are similarities between them and variational autoencoders, they will also be useful for the next part. So it will not be superfluous to meet them too.
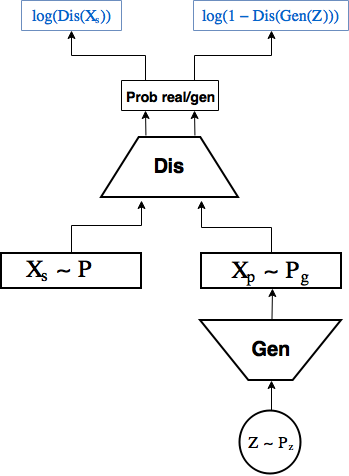
GAN in brief
GANs were first proposed in article [1, Generative Adversarial Nets, Goodfellow et al, 2014] and are now being actively studied. Most state-of-the-art generative models one way or another use adversarial.
GAN scheme:
AutoEncoders in Keras: Conditional VAE
In the last part, we met variational autoencoders (VAE), implemented one on keras, and also understood how to generate images using it. The resulting model, however, had some drawbacks:
Not all the numbers turned out to be well encoded in the latent space: some of the numbers were either completely absent or were very blurry. In between the areas in which the variants of the same number were concentrated, there were generally some meaningless hieroglyphs.
It was difficult to generate a picture of a given digit. To do this, one had to look into what area of the latent space the images of a specific digit fell into, and to sample it from somewhere there, and even more so it was difficult to generate a digit in some given style.
In this part, we will see how only by slightly complicating the model to overcome both these problems, and at the same time we will be able to generate pictures of new numbers in the style of another digit - this is probably the most interesting feature of the future model.
Partially Differential Equations in Tensorflow
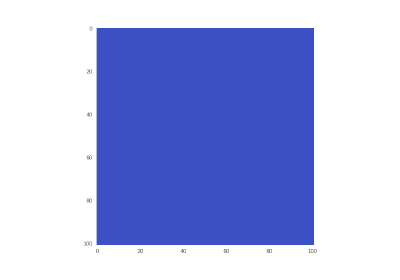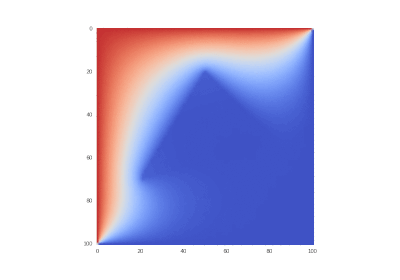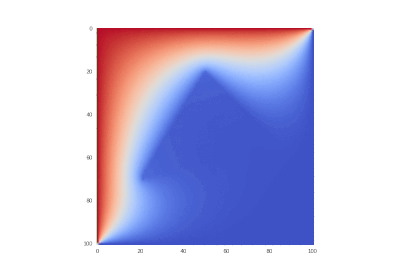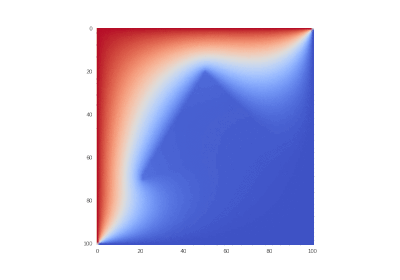
Inspired by a course on parallel computing in my university and just after got acquainted with Tensorflow, I wrote this article as the result of a curiosity to apply framework for deep learning to the problem that has nothing to do with neural networks, but is mathematically similar.
Continue